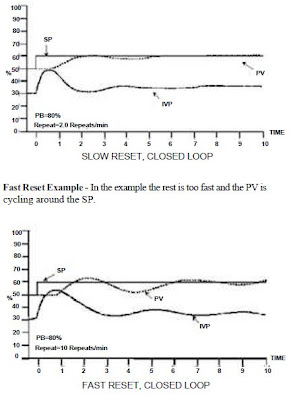
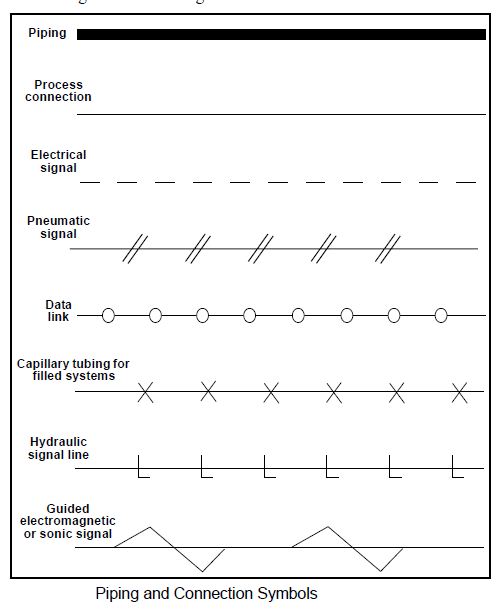
controls one process variable by sending signals to a controller of a
different loop that impacts the process variable of the primary loop.
For example, the primary process variable may be the temperature of
the fluid in a tank that is heated by a steam jacket (a pressurized steam
chamber surrounding the tank). To control the primary variable
(temperature), the primary (master) controller signals the secondary
(slave) controller that is controlling steam pressure. The primary
controller will manipulate the setpoint of the secondary controller to
maintain the setpoint temperature of the primary process variable
(Figure 7.17).

When tuning a control loop, it is important to take into account the
presence of multivariable loops. The standard procedure is to tune the
secondary loop before tuning the primary loop because adjustments
to the secondary loop impact the primary loop. Tuning the primary
loop will not impact the secondary loop tuning.
FEEDFORWARD CONTROL
Feedforward control is a control system that anticipates load
disturbances and controls them before they can impact the process
variable. For feedforward control to work, the user must have a
mathematical understanding of how the manipulated variables will
impact the process variable. Figure 7.19 shows a feedforward loop in
which a flow transmitter opens or closes a hot steam valve based on
how much cold fluid passes through the flow sensor.
An advantage of feedforward control is that error is prevented, rather
than corrected. However, it is difficult to account for all possible load
disturbances in a system through feedforward control. Factors such as
outside temperature, buildup in pipes, consistency of raw materials,
humidity, and moisture content can all become load disturbances and
cannot always be effectively accounted for in a feedforward system.
In general, feedforward systems should be used in cases where the
controlled variable has the potential of being a major load disturbance
on the process variable ultimately being controlled. The added
complexity and expense of feedforward control may not be equal to
the benefits of increased control in the case of a variable that causes
only a small load disturbance.
FEED FORWARD PLUS FEEDBACK
Because of the difficulty of accounting for every possible load
disturbance in a feedforward system, feedforward systems are often
combined with feedback systems. Controllers with summing
functions are used in these combined systems to total the input from
both the feedforward loop and the feedback loop, and send a unified
signal to the final control element. Figure 7.20 shows a
feedforward-plus-feedback loop in which both a flow transmitter and
a temperature transmitter provide information for controlling a hot
steam valve.
CASCADE CONTROL
Cascade control is a control system in which a secondary (slave)
control loop is set up to control a variable that is a major source of load
disturbance for another primary (master) control loop. The controller
of the primary loop determines the setpoint of the summing contoller in
the secondary loop (Figure 7.25).
BATCH CONTROL
Batch processes are those processes that are taken from start to finish
in batches. For example, mixing the ingredients for a juice drinks is
often a batch process. Typically, a limited amount of one flavor (e.g.,
orange drink or apple drink) is mixed at a time. For these reasons, it is
not practical to have a continuous process running. Batch processes
often involve getting the correct proportion of ingredients into the
batch. Level, flow, pressure, temperature, and often mass
measurements are used at various stages of batch processes.
A disadvantage of batch control is that the process must be frequently
restarted. Start-up presents control problems because, typically, all
measurements in the system are below setpoint at start-up. Another
disadvantage is that as recipes change, control instruments may need
to be recalibrated.
RATIO CONTROL
Imagine a process in which an acid must be diluted with water in the
proportion two parts water to one part acid. If a tank has an acid
supply on one side of a mixing vessel and a water supply on the other,
a control system could be developed to control the ratio of acid to
water, even though the water supply itself may not be controlled. This
type of control system is called ratio control (Figure 7.26). Ratio
control is used in many applications and involves a contoller that
receives input from a flow measurement device on the unregulated
(wild) flow. The controller performs a ratio calculation and signals the
appropriate setpoint to another controller that sets the flow of the
second fluid so that the proper proportion of the second fluid can be
added.
Ratio control might be used where a continuous process is going on
and an additive is being put into the flow (e.g., chlorination of water).
SELECTIVE CONTROL
Selective control refers to a control system in which the more
important of two variables will be maintained. For example, in a
boiler control system, if fuel flow outpaces air flow, then
uncombusted fuel can build up in the boiler and cause an explosion.
Selective control is used to allow for an air-rich mixture, but never a
fuel-rich mixture. Selective control is most often used when
equipment must be protected or safety maintained, even at the cost of
not maintaining an optimal process variable setpoint.
FUZZY CONTROL
Fuzzy control is a form of adaptive control in which the controller
uses fuzzy logic to make decisions about adjusting the process.Fuzzy
logic is a form of computer logic where whether something is or is
not included in a set is based on a grading scale in which multiple
factors are accounted for and rated by the computer. The essential
idea of fuzzy control is to create a kind of artificial intelligence that
will account for numerous variables, formulate a theory of how to
make improvements, adjust the process, and learn from the result.
Fuzzy control is a relatively new technology. Because a machine
makes process control changes without consulting humans, fuzzy
control removes from operators some of the ability, but none of the
responsibility, to control a process.